Olympics skateboarding technique is now physics-optimized

As of 2021, skateboarding is an Olympic sport, which actually somehow makes it cooler. That's weird right? Taking a sport from the X Games, an oversold but still fun 1990s event that gave outsider sports a platform, to the Olympics, a bloated and corrupt mess, shouldn't work. But somehow, like snowboarding, extreme sports at the Olympics rock! Check out 14 year old Australian Arisa Trew winning a gold medal yesterday! Actually all of the medalists were teenagers, a message from the universe delivered directly into your heart that you are now old.

I'm learning this at the same time as you, but skateboarders "pump." That is, when a skateboarder goes down a hill or a ramp, to increase their speed they squat and stand repeatedly, up and down, to build speed. This is pumping. You can see Trew do it in her performance repeatedly (see about 1:43 for a good example, I apologize but NBC does not allow us to embed their YouTube videos). Here's a full tutorial:

Like anything, skateboarders worked out pumping like how most humans figure things out: trial-and-error. Pumping your knees up and down generates forward momentum and that's all there is to it.

We can do better, said a group of physicists based in Switzerland and Japan, in a new paper in Physical Review Research published on August 5th. In it, the researchers considered the optimal strategies for moving pendulums and swings (imagine kicking and leaning on a swing as a child, similar idea) and used similar ideas to port them over to skateboards (all images courtesy of the researchers):

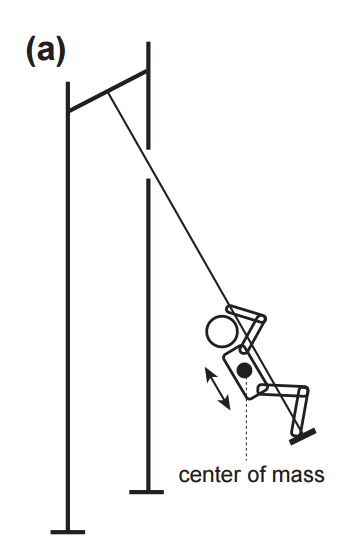
They imagine a skateboard half-pipe as essentially a swinging pendulum with a variable length flat center buttressed on both sides by a curve. Like this guy:

What the researchers realized is less a standard protocol for how to pump and generate speed for everyone everywhere (that depends on each skaters height and the length and type of pipe they are skating on, according to the following equation, which I will not define:

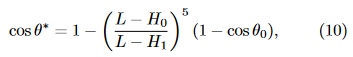
Instead, testing two real life human skaters, a professional with eleven years of skating experience and an amateur with two years, they found a generalized strategy. The acceleration (in meters/second, the bottom line graph) is greatest when the skater is coming down the first half of the pipe, followed by one up-and-down pump (seen in h, height in meters, the first line graph) followed by another pump as they go up the other side, for a pipe with a flat region of about three meters and a curve of about two meters in diameter on both sides.

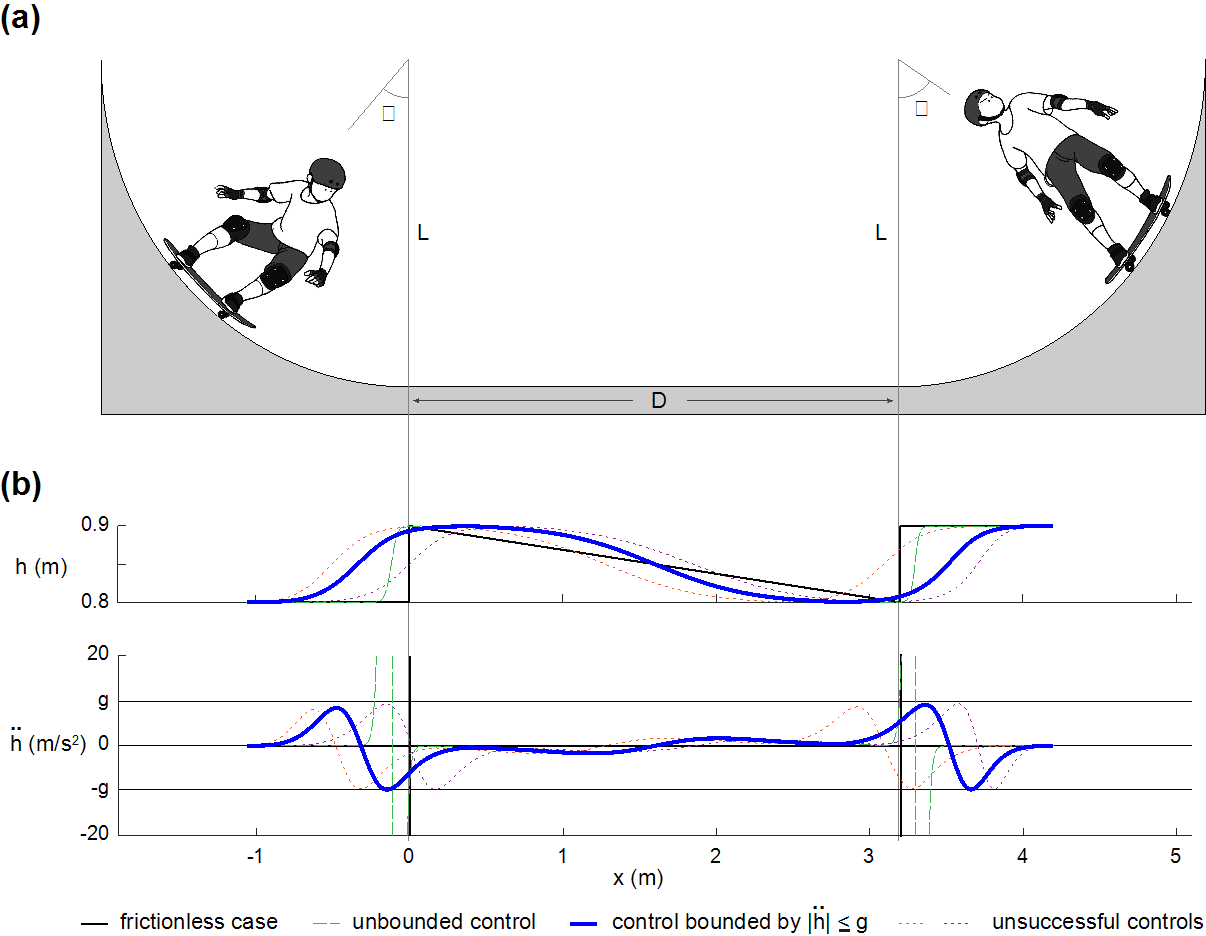
They even found that the professional skater was mathematically better at keeping their up-and-down height and acceleration closer to this idealized skater than the amateur skater was. This seen in the smaller error the professional skater achieves, in the reduced distance between the pink line in Figure D shown here, which represents the theoretical optimal strategy, overlain with the real-life acceleration of the skaters, the black lines:

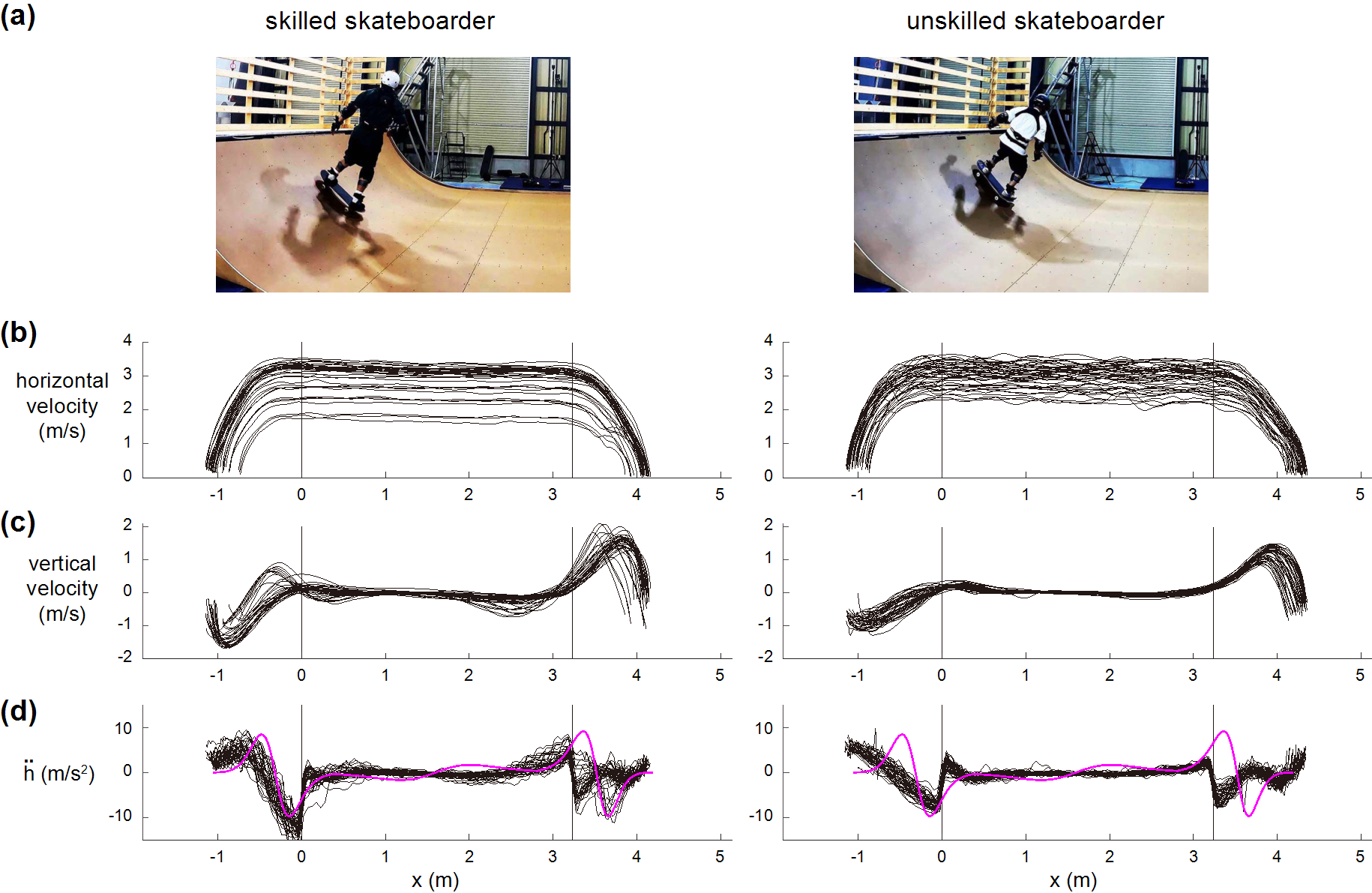
There's more deviation from the "unskilled" skater on the right. I personally fell asleep in every physics class I ever took (two of them) but I'll be taking these results down to the skate park to see what the kids say. Hey kids!